Le zitterbewegung est(-il) un mouvement quantique (réel?) [une série de rebonds sur le vide du champ de Higgs] {entre les deux feuillets d'un espace non commutatif} imaginaire

Bossons sur le boson (8^ème épisode)
//ce billet a été légèrement retouché le 17/11/2019 (titre & ajout d'un paragraphe sur le modèle physico-mathématique dérivé de la géométrie commutative tel qu'exposé son fondateur : Alain Connes)

Le zitterbewegung : un vieux problème mis sous le tapis ... 
C'est du moins l'avis de John Huth physicien et blogueur sur le site Quantum Diaries ...

Paul Dirac was a theoretical physicist who is best known for his famous equation describing the motion of particles like electrons. He successfully combined two pillars of modern theory: quantum mechanics, which describes particles as a wave with special relativity, which takes the speed of light to be a fundamental constant of nature.

When he put these two factors together, his equation had some strange properties. At first blush, you find that electrons have this strange motion that’s called ‘zitterbewegung’; German for ‘trembling motion’. This is a very rapid oscillation of electrons at the speed of light, which doesn’t seem to really happen and would lead to odd results. This was more or less brushed under the rug.

John Huth, Worshipping at the Fed Ex drop box, 28/10/2011

...  avis qui n'est pas partagé par un autre blogueur, Lubos Motl :

I am very surprised that it is not generally understood that the whole idea of Zitterbewegung is nonsense arising from an invalid physical interpretation of an equation. Just to be sure, Erwin Schrödinger ... has tried to solve the Dirac equation once Dirac wrote it down. And he combined some "positive-energy" and "negative-energy" solutions. Because their energies differ at least by 2mc², not too surprisingly, by the interference of these two components, one "gets" some observables that oscillate with the gigantic angular frequency 2mc²/ℏ. 

However, nothing like that may occur in the real world because the single-particle interpretation of the Dirac equation – with positive- as well as negative-energy solutions allowed – simply doesn't apply and cannot apply to the real world. As Dirac quickly understood (while Schrödinger didn't), the negative-energy solutions have to be treated differently...

Lubos Motl, why Zitterbewegung is unphysical, 28/10/2011 

... mais un problème qui bouge peut-être encore !
Entre deux feuillets d'un espace-temps non commutatif ? La preuve par les mots avec le titre d'une conférence (dont le contenu n'est malheureusement pas accessible sur la toile est partiellement disponible sur la toile) et un extrait d'un article de Robert Brout un des pères du boson de Higgs :

"The gauged zitterbewegung: Connes' constructions of the standard model"

R. Brout, International School of Subnuclear Physics, Erice, Italy Août 1999

Now for one of Connes’ main ideas. Scalars are gauge bosons that serve as connections in a manifold comprised of 2 points: left (L) and right (R), which I now explain at length. Fermions, in the absence of mass, are displaced in space-time, on two different surfaces L and R, through the action of the Dirac operator. The usual Yang-Mills fields (YM) supply connections on these surfaces so as to allow internal symmetries to be gauged. The vector and axial currents coupled to the YM are sums of bilinears in L or R fermions and do not mix L and R. i.e. the coupling keeps an L (R) fermion on the L (R) surface. The role of mixing L and R is taken on by the scalars through a coupling (ψ_L⁺ψ_Rφ +h.c.). The bilinear ψ_L⁺ψ_R is a sort of current between the 2 corresponding points L and R at the same space-time point x^μ, φ being the “gauge scalar”. The thought is not only engaging, but it ties in most elegantly with Connes’ rewriting of geometry on discrete spaces in terms of axioms which permit a natural generalization of all continuum concepts. These discrete spaces can be composed of but 2 points -L and R in particular, and so are applicable to SM gauge geometry.

R. Brout, Notes on Connes’ Construction of the Standard Model, 27/06/1997

Pour une exposition en français des idées et du modèle physico-mathématique présentées ci-dessus, voici des extraits du livre d'Alain Connes Géométrie non commutative et de son article fondateur sur l'application de son grand oeuvre à la physique du méchanisme de Brout-Englert-Higgs.

...(work in progress)

Y a-t-il d'autres traces d'un lien métaphorique entre zitterbewegung et boson de Higgs ?

En cherchant sur internet voici la réponse d'un fameux mathématicien Roger Penrose:

Roger Penrose (in "The Road to Reality") and Tony Zee (in "QFT in a Nutshell") show that the Dirac Lagrangian can be decomposed into two massless fields (thus propagating at c), one with left handed helicity and one right handed, coupled by a parameter proportional to the rest-mass of the particle. Penrose calls the left handed field the "zig" particle and the right handed one the "zag" particle. The zigzagging (which occurs on average at the de Broglie frequency) allows/forces the particle's average velocity to be less than c, and in its rest frame, results in the direction of its spin remaining constant. While both the zig and zag fields interact equally electromagnetically, only the zig field interacts via the weak interaction. Penrose states that the conversion of a zig into a zag and vice versa can be viewed as an interaction with the Higgs field.

 Kit Adams, Electron's zitterbewegung, Physics Forums Oct 12 2006

Une science métaphorique porte(-t-elle) forcément à confusion (Monsieur Zee?)

Le risque est grand en tout cas si l'on en croit cet avertissement d'un spécialiste de la théorie quantique des champs :

In closing this chapter [on quantizing the Dirac field] let me ask you some rhetorical questions. Did I speak of an electron going backward in time? Did I mumble something about a sea of negative energy electrons? This metaphorical language, when used by brilliant minds, the likes of Dirac and Feynman, was evocative and inspirational, but unfortunately confused generations of physics students and physicists. The presentation given here is in the modern spirit, which seeks to avoid these potentially confusing metaphors. 

Anthony Zee, Poetic but confusing metaphors, 2003

Certaines images ont pourtant bien un pouvoir heuristique (n'est ce pas Monsieur Feynman?)
En oubliant pour un temps la référence explicite au zitterbewegung, voici une présentation du mécanisme de Higgs, en bande dessinée ou presque, par un brillant blogueur du site Quantum Diaries :

one can formulate our entire Feynman diagram program in terms of completely massless particles. In such a picture, particles like the top quark or Z boson undergo lots of the aforementioned two-point “mass” interactions and so are observed to have larger masses. Heuristically, heavy particles barrel along and have lots of these two-point interactions:

For comparison, a light particle like the electron would have fewer of these interactions. Their motion (again, heuristically) looks more like this:

We should remember that each of these crosses is really a terminated Higgs line. To use some fancy parlance which will come up in a later post, we say that the Higgs has a “vacuum expectation value” and that these particles are bumping up against it. The above pictures are just ‘cartoons’ of Feynman diagrams, but you can see how this seems to convey a sense of “inertia.” More massive particles (like the top quark) are harder to push around because they keep bumping up against the Higgs. Light particles, like the electron, don’t interact with the Higgs so much and so can be pushed more easily. 

In this sense, we can think of all particles as being massless, but their interactions with the Higgs generates a two-point interaction which is effectively a mass. Particles which interact more strongly with the Higgs have more mass, while particles which interact weakly with the Higgs have less mass. In fact, once we assume this, we might as well drop all of the silly crosses on these lines—and then we’re left with the usual Feynman rules (with no terminating Higgs lines) that are usually presented.

 Flip Tanedo, A diagrammatic hint of masses from the Higgs, 5/05/2011

Et de bons dessins ont toujours une valeur pédagogique (merci Monsieur Tanedo!)
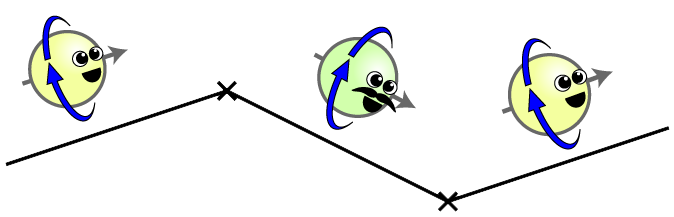
Les petits diagrammes ci-dessus deviennent une vrai BD ci-dessous et l'analogie entre zitterbewegung et mécanisme de Higgs se renforce :

An "electron" propagating in space and interacting with the Higgs field. Note that the Higgs-induced mass term connects an electron with an anti-positron. This means that the two types of particles are exhibiting quantum mixing. Note that in this picture the blue arrow represents helicity (it is conserved), whereas the mustache (or non-mustache) represents chirality. The mass insertions flip chirality, but maintain helicity.

This is very important; two completely different particles (the electron and the anti-positron) are swapping back and forth. What does this mean? The physical thing which is propagating through space is a mixture of the two particles. When you observe the particle at one point, it may be an electron, but if you observe it a moment later, the very same particle might manifest itself as an anti-positron! This should sound very familiar, it’s the exact same story as neutrino mixing (or, similarly, meson mixing).

Let us call this propagating particle is a “physical electron.” The mass-basis-electron can either be an electron or an anti-positron when you observe it; it is a quantum mixture of both.

Flip Tanedo, Helicity, Chirality, Mass, and the Higgs, 5/05/2011